Cheat Sheet: Model Development

 

Cheat Sheet: Model Development

Process	Description	Code Example
Linear Regression	Create a Linear Regression model object	1 2 from sklearn.linear_model import LinearRegression lr = LinearRegression()
Train Linear Regression model	Train the Linear Regression model on decided data, separating Input and Output attributes. When there is single attribute in input, then it is simple linear regression. When there are multiple attributes, it is multiple linear regression.	1 2 3 X = df[[‘attribute_1’, ‘attribute_2’, ...]] Y = df['target_attribute'] lr.fit(X,Y)
Generate output predictions	Predict the output for a set of Input attribute values.	1 Y_hat = lr.predict(X)
Identify the coefficient and intercept	Identify the slope coefficient and intercept values of the linear regression model defined by 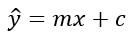 Where m is the slope coefficient and c is the intercept.	1 2 coeff = lr.coef intercept = lr.intercept_
Residual Plot	This function will regress y on x (possibly as a robust or polynomial regression) and then draw a scatterplot of the residuals.	1 2 3 import seaborn as sns sns.residplot(x=df[[‘attribute_1’]], y=df[[‘attribute_2’]])
Distribution Plot	This function can be used to plot the distribution of data w.r.t. a given attribute.	1 2 3 import seaborn as sns sns.distplot(df['attribute_name'], hist=False) # can include other parameters like color, label and so on.
Polynomial Regression	Available under the numpy package, for single variable feature creation and model fitting.	1 2 3 4 5 6 f = np.polyfit(x, y, n) #creates the polynomial features of order n p = np.poly1d(f) #p becomes the polynomial model used to generate the predicted output Y_hat = p(x) # Y_hat is the predicted output
Multi-variate Polynomial Regression	Generate a new feature matrix consisting of all polynomial combinations of the features with the degree less than or equal to the specified degree.	1 2 3 4 from sklearn.preprocessing import PolynomialFeatures Z = df[[‘attribute_1’,’attribute_2’,...]] pr=PolynomialFeatures(degree=n) Z_pr=pr.fit_transform(Z)
Pipeline	Data Pipelines simplify the steps of processing the data. We create the pipeline by creating a list of tuples including the name of the model or estimator and its corresponding constructor.	1 2 3 4 5 6 7 8 9 from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler Input=[('scale',StandardScaler()), ('polynomial', PolynomialFeatures(include_bias=False)), ('model',LinearRegression())] pipe=Pipeline(Input) Z = Z.astype(float) pipe.fit(Z,y) ypipe=pipe.predict(Z)
R^2 value	R^2, also known as the coefficient of determination, is a measure to indicate how close the data is to the fitted regression line. The value of the R-squared is the percentage of variation of the response variable (y) that is explained by a linear model. a. For Linear Regression (single or multi attribute) b. For Polynomial regression (single or multi attribute)	a. 1 2 3 4 X = df[[‘attribute_1’, ‘attribute_2’, ...]] Y = df['target_attribute'] lr.fit(X,Y) R2_score = lr.score(X,Y) b. 1 2 3 4 from sklearn.metrics import r2_score f = np.polyfit(x, y, n) p = np.poly1d(f) R2_score = r2_score(y, p(x))
MSE value	The Mean Squared Error measures the average of the squares of errors, that is, the difference between actual value and the estimated value.	1 2 from sklearn.metrics import mean_squared_error mse = mean_squared_error(Y, Yhat)